La fractalidad es una propiedad presente en cada uno de los elementos de la naturaleza. En geología, un fractal puede observarse en una fábrica petrológica, facies sedimentarias o sistemas de fallas debido a que sus geometrías son invariables respecto a la escala. La cuantificación de las características fractales, es decir, las dimensiones fractales, tienen relación directa con la complejidad del sistema estructural: si tales dimensiones tienden a incrementarse también aumenta la probabilidad de encontrar una mayor interconectividad entre estructuras o permeabilidad secundaria (Zhao y otros, 2011). Tal como describe Blenkinsop (2004), la distribución espacial de los depósitos minerales y sus modelos de mineralización tienen una naturaleza fractal (Blenkinsop, 2004). Donde la unidad de medida es la dimensión fractal la cual varía entre 0 y 2, además de que este valor tiene una relación indirecta con la acumulación mineral (Blenkinsop, 2004; Ford y Blenkinsop, 2008). En tal sentido, el empleo de las dimensiones fractales en geología estructural sirve como un análisis complementario de la cartografía geológica y del estudio de estructuras tectónicas en sitios donde, por ejemplo, los datos microestructurales se encuentren muy dispersos o donde no exista una continuidad clara de las estructuras tectónicas.
Los fractales fueron descritos por primera vez en los años 70 por Benoit Mandelbrot quien describía a los elementos complejos de la naturaleza desde un enfoque abstracto en lugar de la forma clásica euclidiana. No fue hasta el año 1983 que el mismo autor realizó correcciones a sus postulados. También sugirió el uso probable de los fractales en Geología (Mandelbrot, 1977 y 1983), especialmente en la distribución espacial de los depósitos minerales. En efecto, la geometría abstracta de Mandelbrot (1983) considera que los objetos naturales como montañas, árboles o las nubes no son simples líneas ni polígonos. De acuerdo con estas aseveraciones, las estructuras tectónicas como fallas, vetas y fracturas, desde cierto punto de vista, tienen naturaleza fractal (Tchalenko, 1970; Walsh y otros, 1991; Childs; 2017).
Ya después de los años 80 y en la década actual, el empleo de las dimensiones fractales ha sido un tema bastante recurrente en la exploración geológica-minera (Turcotte, 1991; Blenkinsop, 2004; Ford y Blenkinsop, 2008; Austin y Blenkinsop, 2009; Gumiel y otros, 2010). El método más usual para la determinación de las dimensiones fractales es conocido como la técnica del box-counting o “conteo de celdas”. Para el análisis de las estructuras tectónicas, se requiere establecer un número “N(r)” de celdas que contengan a todas las estructuras. El parámetro “r” corresponde al valor numérico de la dimensión escogida para las celdas que serán objeto de conteo; mientras que el valor de la dimensión fractal “D” es el coeficiente de determinación obtenido a partir de la regresión lineal entre los logaritmos de “N(r)” y “r”, respectivamente.
En la cartografía geológica, se suele identificar fallas, vetas o fracturas para conocer si fueron formadas por aperturas o cierres tectónicos. Su mapeo llega a complicarse cuando tienen muestran interconectividad debido a la intersección de dos o más direcciones dentro de sus zonas de cizalla. Estas complejidades pueden estar relacionadas a flexiones, torciones en los ángulos de buzamiento, variación lateral en la potencia de vetas, o a sobreimposición tectónica. Para los estudios de geología estructural, surge la problemática de conocer qué tanto y en qué amplitud una tectónica de desgarre, extensional o compresional pudo haber influenciado en la deformación de los afloramientos rocosos cercanos. Las estructuras tectónicas presentan interconexiones entre sí, irregularidades, rugosidades y cinemáticas que influyen en la permeabilidad secundaria. Es posible evaluar tal permeabilidad en vetas auríferas y en rocas polifracturadas asociadas a pórfidos de cobre-molibdeno. Valores de dimensiones fractales cercanos a 0 indican baja permeabilidad secundaria, mientras que valores mayores a 1 o cercanos a 2 indican un mayor grado de fracturamiento o cizallamiento, el cual, puede estar relacionado a anomalías de elementos metálicos.
En la siguiente imagen se tiene un ejemplo de mapeo geológico-estructural y el empleo de las dimensiones fractales:
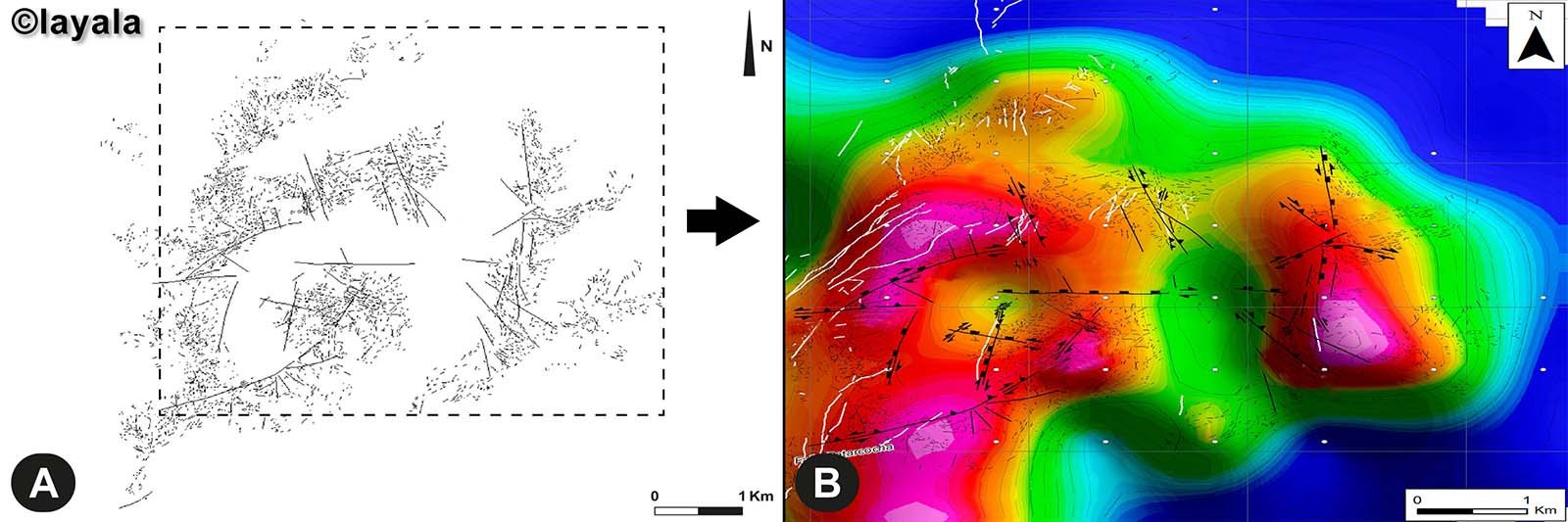
Consideraciones importantes
En el empleo de las dimensiones fractales en geología estructural se debe considerar:
-Las zonas de cizalla que tienden a ser más permeables tienden a poseer valores de dimensiones fractales “D” más altos y/o cercanos a 2, mientras que las menos permeables tienen valores iguales o menores a 1. Así, la noción fractal de la complejidad/interconectividad, irregularidad, rugosidad y cinemática de estructuras sirve como una herramienta complementaria para la exploración minera.
-El uso de la técnica del box-counting enfocada a la determinación de las dimensiones fractales tiene sus limitaciones cuando las estructuras tectónicas no tienen un comportamiento fractal. Esto puede ocurrir en el caso de sistemas estructurales que son analizados con un número pobre (menor a 3) de dimensiones de celda (r) y cuyas magnitudes de dimensión sean cercanas, iguales o más grandes que la red de estructuras a estudiar. De forma general, un método sencillo de validar la geometría fractal de un conjunto de elementos es verificando que el coeficiente de determinación sea cercano a 1, lo cual hace entender que la dispersión de valores Log N(r) vs Log r sea una tendencia lineal. No obstante, pueden existir diversos factores que determinen un comportamiento no fractal en la naturaleza. Por lo que siempre es importante considerar otros parámetros directos de campo como es la medición cualitativa de la cinemática tectónica de las estructuras, el mapeo de discontinuidades, el estilo de mineralización, el tipo de alteración, entre otros.
-El empleo de las dimensiones fractales no solo es útil para los estudios de geología estructural, sino también en trabajos de minería de superficie, subterránea o de tajos abiertos. La metodología fractal también es aplicable para la interpolación 2D de una buena densidad de estructuras que puedan proyectarse a lo largo de secciones topográficas.
-En regiones o áreas particulares donde se tenga una geología fuertemente influenciada por la tectónica, el análisis de las dimensiones fractales para la determinación de la permeabilidad secundaria tal como sucede en márgenes activas (P. Ej. Los Andes) no puede tomarse a la ligera. De forma que las zonas de cizalla extensionales y/o compresionales deberían correlacionarse con los valores altos y/o bajos de las dimensiones fractales, respectivamente.
-El empleo de las dimensiones fractales no es una metodología que trabaja de forma aislada. Sus resultados deben tener coherencia con otros datos provenientes de características litológicas, mineralógicas, de alteraciones, estructurales, etc.).
-Las estructuras tectónicas con cinemáticas compresivas, o de desgarre asociadas a compresión pueden presentar permeabilidades secundarias de poco interés, y acompañado a este cierre tectónico, las vetas en consecuencia presentan menor potencia.